Explaining Modular Representations with Range

Original Paper: Range, Not Independence, Drive Modularity in Biologically Inspired Representations

Core Idea

The central question of this paper is: what determines whether a neural system develops modular representations (where neurons respond to single, independent features) or mixed-selectivity (where neurons respond to a complex combination of features)?

This work challenges the traditional theory that “statistical independence” is the deciding factor. Instead, it proposes a new, more general condition called “Range of Independence”. The authors mathematically and empirically demonstrate that this property—specifically, whether the full range of extreme values (the “corners”) of source data is present—dictates which representation is more energy-efficient.

Summary of the Paper

Modularity vs. Mixed Selectivity

• Modularity: A neuron responds to only one source or variable. Examples include orientation-selective cells in the visual cortex or grid cells in the entorhinal cortex. This is a classic view in neuroscience.
• Mixed Selectivity: A neuron responds to a combination of multiple, diverse variables. This is common in higher cognitive areas like the Prefrontal Cortex (PFC) and is crucial for complex tasks and context-dependent decisions.

”Range of Independence”

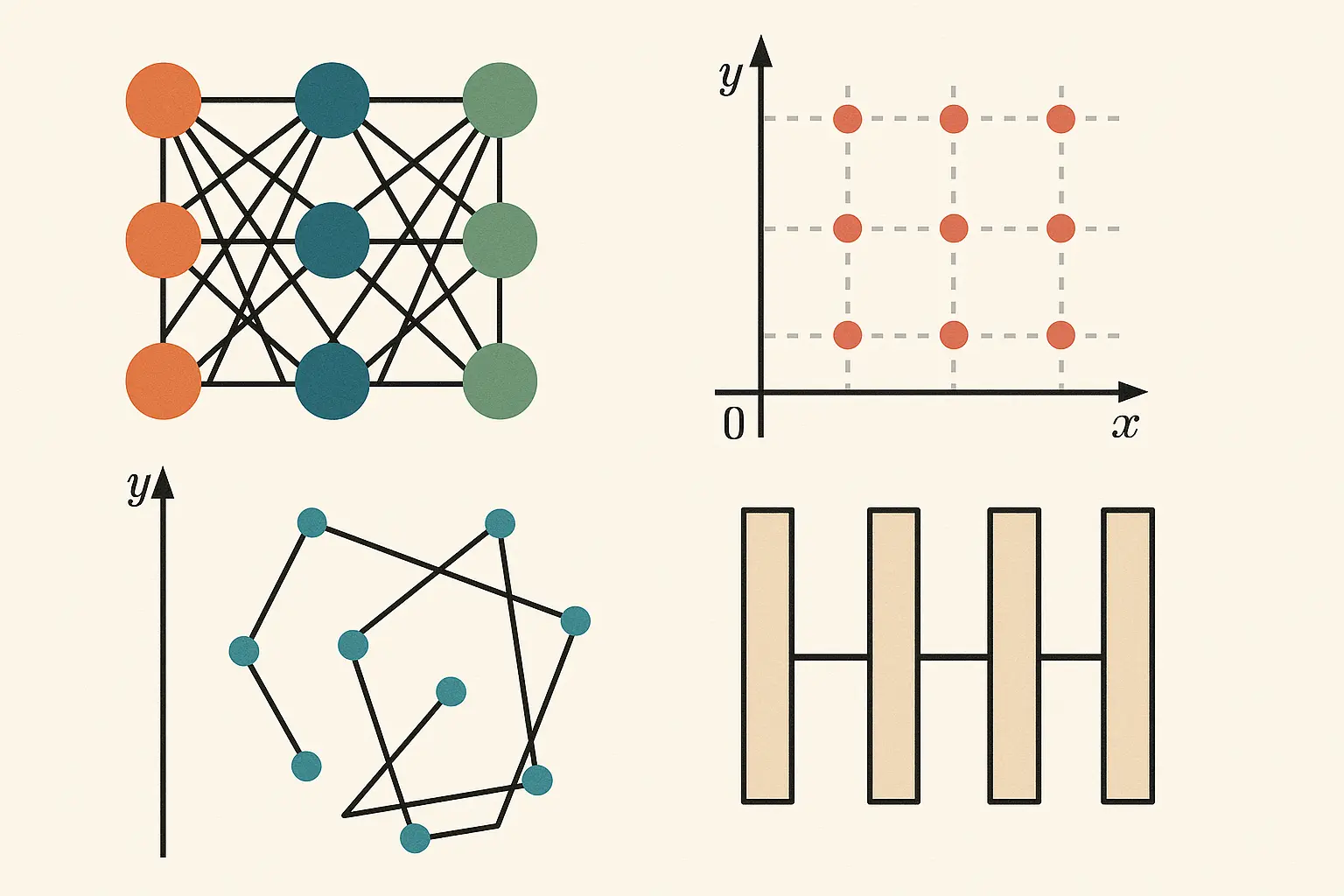
• The paper uses a linear autoencoder model with biological constraints (like non-negativity, representing firing rates) to test this idea.
• The key finding is that modular representations are more energy-efficient if and only if the source data is “range independent”.
• “Range Independent” means that the extreme values of all sources can occur simultaneously (e.g., the “corners” of a square distribution exist). If the corners are missing (e.g., the distribution is a circle or a diagonal line), the data is “range dependent,” and a mixed representation becomes more efficient.

Generalization to Non-linear & Recurrent Models

• The theory is shown to hold true for more complex models, including non-linear autoencoders (using ReLU) and Recurrent Neural Networks (RNNs).
• In RNNs processing dynamic inputs (like sine waves), the frequency ratios determine the range independence. Irrational ratios lead to range-independent distributions (a full square) and modular hidden states, while harmonic ratios lead to range-dependent distributions (a line or curve) and mixed states.

Biological Applications & Grid Cells

• This theory is used to explain conflicting experimental data on grid cells.
• Some studies show grid cells are highly modular, while others show they become “mixed” and respond to task-relevant variables (like rewards or goals).
• The paper argues this isn’t a contradiction. The task structure itself (e.g., whether rewards are “factorized” from location or “entangled”) changes the “range of independence” of the inputs, forcing the network to adopt either a modular or mixed strategy for efficiency.
• It also cautions that some observations of mixed selectivity in biological data might be an illusion caused by unobserved variables.

Key Discussion Points

1. ReLU as a Biologically Plausible Model: The group discussed why the ReLU activation function, used in the paper’s non-linear models, is a good choice for biological simulations. Unlike sigmoid, ReLU is:

   • Biologically Plausible: Its thresholded, all-or-nothing activation mirrors how biological neurons remain silent until input exceeds a threshold, then fire in response.
   • Sparse and Efficient: It outputs zero for many inputs, promoting sparsity, which is energy-efficient and similar to brain activity.
   • Stable for Learning: It does not suffer from the vanishing gradient problem.
   • An interesting parallel: One speaker noted that a Hodgkin-Huxley neuron model behaves like a ReLU under low-noise conditions but like a sigmoid under high-noise conditions.

2. Why the Brain Uses Both Modularity and Mixed Selectivity: The discussion concluded that the brain employs both strategies for different purposes, and the paper’s theory provides a new energy-based reason why.

   • Modularity is ideal for robust, reusable, and disentangled representations, especially for sensory inputs that are “range independent” (e.g., all visual orientations and all positions are possible).
   • Mixed Selectivity is ideal for flexible, complex, and context-dependent computations (e.g., in the PFC), which the paper suggests is more energy-efficient for “range-dependent” inputs.

3. The Limits of Reductionism: The group debated whether a purely reductionist approach can ever fully explain the brain.

   • Dynamic vs. Static: A key critique was that many neuroscience experiments are “static” (studying a fixed task) and may only be capturing the “byproducts” or “shadows” of intelligence, rather than the dynamic learning process itself.
   • Embodiment and Emergence: The brain is an “open system” that interacts with a body and environment, exhibiting emergent properties that can’t be understood by studying its parts in isolation.

4. Neural Representations are Flexible, Not Fixed: This point was illustrated with grid cells as a prime example of task-dependent representation.

   • Evidence from Rat Models: In rats with amyloid plaques (modeling Alzheimer’s), grid cells fail at path integration. However, they don’t stop working; they switch strategies, changing their firing pattern from hexagonal to square (90-degree) to align with visual cues like walls.
   • Human VR Parallel: Humans at high risk for Alzheimer’s show the same path integration deficit in open VR but perform normally when visual landmarks are available. They also navigate closer to these landmarks, suggesting a similar compensatory strategy.
   • Conclusion: This suggests representations are not fixed but are flexible “bases” (inductive biases) that the brain adopts to solve the specific task at hand with the available information.

Original Video